В одном специальном случае дадим определение вероятности события для
случайного эксперимента с несчетным множеством исходов.
Если между множеством элементарных исходов случайного эксперимента и
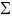
множеством точек некоторой плоской фигуры (сигма большая) можно установить
взаимно-однозначное соответствие, а также можо установить взаимно-однозначное
соответствие между множеством элементарных исходов, благоприятствующих
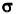
событию А, и множеством точек плоской фигуры (сигма малая), являющейся частью
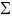
фигуры , то



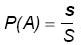
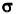
где s — площадь фигуры , S — площадь фигуры .
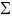
Пример. Два человека обедают в столовой, которая открыта с 12 до 13 часов.
Каждый из них приходит в произвольный момент времени и обедает в течение 10
минут. Какова вероятность их встречи?
Пусть x — время прихода первого в столовую, а y — время прихода второго
(12x13; 12y13).