Статистическая проверка гипотез является вторым после
статистического оценивания параметров распределения и в то же время
важнейшим разделом математической статистики.
Методы математической статистики позволяют проверить
предположения о законе распределения некоторой случайной величины
(генеральной совокупности), о значениях параметров этого закона
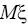
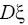
(например , ), о наличии корреляционной зависимости между
случайными величинами, определенными на множестве объектов одной и
той же генеральной совокупности.
Пусть по некоторым данным имеются основания выдвинуть
предположения о законе распределения или о параметре закона
распределения случайной величины (или генеральной совокупности, на
множестве объектов которой определена эта случайная величина). Задача
заключается в том, чтобы подтвердить или опровергнуть это
предположение, используя выборочные (экспериментальные) данные.
Гипотезы о значениях параметров распределения или о
сравнительной величине параметров двух распределений называются
параметрическими гипотезами.
Гипотезы о виде распределения называются непараметрическими
гипотезами.
Проверить статистическую гипотезу – это значит проверить,
согласуются ли данные, полученные из выборки с этой гипотезой.
Проверка осуществляется с помощью статистического критерия.
Статистический критерий – это случайная величина, закон
распределения которой (вместе со значениями параметров) известен в
случае, если принятая гипотеза справедлива. Этот критерий называют
еще критерием согласия (имеется в виду согласие принятой гипотезы с
результатами, полученными из выборки).
Гипотезу, выдвинутую для проверки ее согласия с выборочными
данными, называют нулевой гипотезой и обозначают H₀. Вместе с
гипотезой H₀ выдвигается альтернативная или конкурирующая
гипотеза, которая обозначается H₁. Например:



Пусть случайная величина K – статистический критерий проверки
некоторой гипотезы H₀. При справедливости гипотезы H0 закон
распределения случайной величины K характеризуется некоторой
известной нам плотностью распределения p_K(x).
Выберем некоторую малую вероятность a, равную 0,05 , 0,01 или
еще меньшую. Определим критическое значение критерия K_кp как
решение одного из трех уравнений, в зависимости от вида нулевой и
конкурирующей гипотез: