Повторные независимые испытания. Формула Бернулли.
11 ноября 2008. Разместил: admin
Рассмотрим случай многократного повторения одного и того же испытания или
случайного эксперимента. Результат каждого испытания будем считать не зависящим
от того, какой результат наступил в предыдущих испытаниях. В качестве результатов
или элементарных исходов каждого отдельного испытания будем различать лишь две
возможности:
1) появление некоторого события А;
2) появление события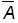 , (события, являющегося дополнением А)
, (события, являющегося дополнением А)
Пусть вероятность P(A) появления события А постоянна и равна p (0<.p<1).
Вероятность P(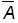 ) события
) события 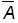 обозначим через q: P(
обозначим через q: P(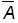 ) = 1- p=q.
) = 1- p=q.
Примерами таких испытаний могут быть:
1) подбрасывание монеты: А - выпадение герба;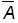 - выпадение цифры.
- выпадение цифры.
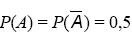 .
.
2) бросание игральной кости: А - выпадение количества очков, равного пяти,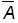
выпадение любого количества очков кроме пяти.
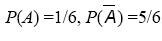
3) извлечение наудачу из урны, содержащей 7 белых и 3 черных шара, одного шара (с
возвращением): А - извлечение белого шара,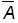 - извлечение черного шара
- извлечение черного шара
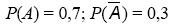
случайного эксперимента. Результат каждого испытания будем считать не зависящим
от того, какой результат наступил в предыдущих испытаниях. В качестве результатов
или элементарных исходов каждого отдельного испытания будем различать лишь две
возможности:
1) появление некоторого события А;
2) появление события
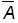 , (события, являющегося дополнением А)
, (события, являющегося дополнением А)Пусть вероятность P(A) появления события А постоянна и равна p (0<.p<1).
Вероятность P(
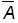 ) события
) события 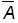 обозначим через q: P(
обозначим через q: P(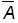 ) = 1- p=q.
) = 1- p=q.Примерами таких испытаний могут быть:
1) подбрасывание монеты: А - выпадение герба;
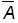 - выпадение цифры.
- выпадение цифры.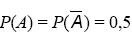 .
.
2) бросание игральной кости: А - выпадение количества очков, равного пяти,
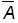
выпадение любого количества очков кроме пяти.
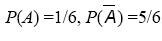
3) извлечение наудачу из урны, содержащей 7 белых и 3 черных шара, одного шара (с
возвращением): А - извлечение белого шара,
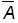 - извлечение черного шара
- извлечение черного шара