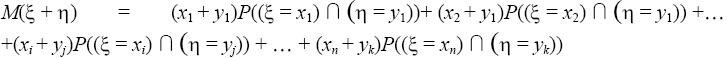Пример. Найти математическое ожидание случайной величины
11 ноября 2008. Разместил: admin
Пример. Найти математическое ожидание случайной величины, заданной
законом распределения
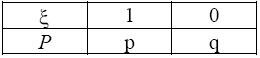
Здесь p + q = 1.
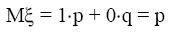
Свойства математического ожидания.
1. Если случайная величина принимает одно и то же значение при всех
принимает одно и то же значение при всех
исходах случайного эксперимента, то есть = С, то её математическое
= С, то её математическое
ожидание равно С.
2. Если М = а, и k – константа, то М(k
= а, и k – константа, то М(k ) = kM
) = kM (математическое
(математическое
ожидание случайной величины, умноженной на число, равно
математическому ожиданию случайной величины, умноженному на
это число).
3. Если М = а, и k – константа, то М(k +
= а, и k – константа, то М(k +  ) = k + M
) = k + M (математическое
(математическое
ожидание суммы случайной величины и числа равно сумме этого
числа и математического ожидания случайной величины).
Выведем формулу для математического ожидания суммы двух случайных
величин и
и  , определённых на одном и том же пространстве элементарных
, определённых на одном и том же пространстве элементарных
исходов и заданных законами распределения

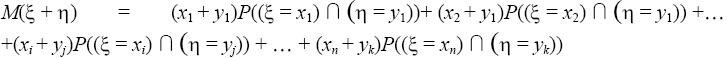
законом распределения
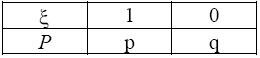
Здесь p + q = 1.
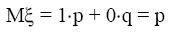
Свойства математического ожидания.
1. Если случайная величина
 принимает одно и то же значение при всех
принимает одно и то же значение при всехисходах случайного эксперимента, то есть
 = С, то её математическое
= С, то её математическоеожидание равно С.
2. Если М
 = а, и k – константа, то М(k
= а, и k – константа, то М(k ) = kM
) = kM (математическое
(математическоеожидание случайной величины, умноженной на число, равно
математическому ожиданию случайной величины, умноженному на
это число).
3. Если М
 = а, и k – константа, то М(k +
= а, и k – константа, то М(k +  ) = k + M
) = k + M (математическое
(математическоеожидание суммы случайной величины и числа равно сумме этого
числа и математического ожидания случайной величины).
Выведем формулу для математического ожидания суммы двух случайных
величин
 и
и  , определённых на одном и том же пространстве элементарных
, определённых на одном и том же пространстве элементарныхисходов и заданных законами распределения