Ковариация
13 ноября 2008. Разместил: admin
Ковариация  * и
* и  * называется коэффициентом корреляции случайных
* называется коэффициентом корреляции случайных
величин и
и  (обозначается
(обозначается 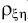 ).
).
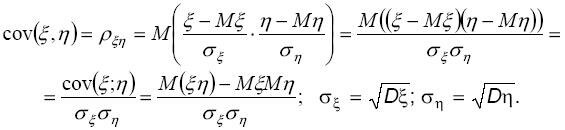
Для независимых и
и 
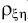 =0, так как в этом случае
=0, так как в этом случае 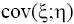 =0
=0
Обратного заключения сделать нельзя. Случайные величины могут быть
связаны даже функциональной зависимостью (каждому значению одной
случайной величины соответствует единственное значение другой случайной
величины), но коэффициент их корреляции будет равен нулю.
Примеры:
1. Пусть случайная величина симметрично распределена около нуля.
симметрично распределена около нуля.
Тогда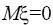 . Пусть
. Пусть 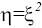 . Тогда
. Тогда 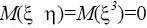 , так
, так 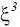 тоже симметрично
тоже симметрично
распределена около нуля. С другой стороны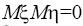 , так как
, так как 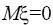 . Таким
. Таким
образом
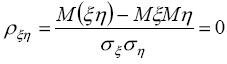
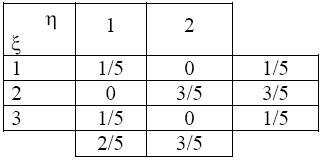
2. Пусть закон совместного распределения случайных величин и
и  задан
задан
таблицей
 * и
* и  * называется коэффициентом корреляции случайных
* называется коэффициентом корреляции случайныхвеличин
 и
и  (обозначается
(обозначается 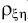 ).
).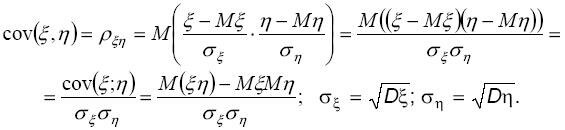
Для независимых
 и
и 
 =0, так как в этом случае
=0, так как в этом случае  =0
=0Обратного заключения сделать нельзя. Случайные величины могут быть
связаны даже функциональной зависимостью (каждому значению одной
случайной величины соответствует единственное значение другой случайной
величины), но коэффициент их корреляции будет равен нулю.
Примеры:
1. Пусть случайная величина
 симметрично распределена около нуля.
симметрично распределена около нуля.Тогда
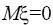 . Пусть
. Пусть 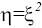 . Тогда
. Тогда 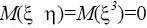 , так
, так 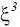 тоже симметрично
тоже симметричнораспределена около нуля. С другой стороны
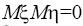 , так как
, так как 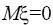 . Таким
. Такимобразом
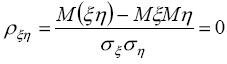
2. Пусть закон совместного распределения случайных величин
 и
и  задан
задантаблицей
