Пусть нам нужно обследовать количественный признак в партии
экземпляров некоторого товара. Проверку партии можно проводить двумя
способами:
1) провести сплошной контроль всей партии;
2) провести контроль только части партии.
Первый способ не всегда осуществим, например, из–за большого
числа экземпляров в партии, из–за дороговизны проведения операции
контроля, из–за того, что контроль связан с разрушением экземпляра
(проверка электролампы на долговечность ее работы).
При втором способе множество случайным образом отобранных
объектов называется выборочной совокупностью или выборкой. Все
множество объектов, из которого производится выборка, называется
генеральной совокупностью. Число объектов в выборке называется
объемом выборки. Обычно будем считать, что объем генеральной
совокупности бесконечен.
Выборки разделяются на повторные (с возвращением) и
бесповторные (без возвращения).
Обычно осуществляются бесповторные выборки, но благодаря
большому (бесконечному) объему генеральной совокупности ведутся
расчеты и делаются выводы, справедливые лишь для повторных выборок.
Выборка должна достаточно полно отражать особенности всех
объектов генеральной совокупности, иначе говоря, выборка должна быть
репрезентативной (представительной).
Выборки различаются по способу отбора.
1. Простой случайный отбор.
Все элементы генеральной совокупности нумеруются и из таблицы
случайных чисел берут, например, последовательность любых 30-ти
идущих подряд чисел. Элементы с выпавшими номерами и входят в
выборку.
2. Типический отбор.
Такой отбор производится в том случае, если генеральную
совокупность можно представить в виде объединения подмножеств,
объекты которых однородны по какому–то признаку, хотя вся
совокупность такой однородности не имеет (партия товара состоит из
нескольких групп, произведенных на разных предприятиях). Тогда по
каждому подмножеству проводят простой случайный отбор, и в выборку
объединяются все полученные объекты.
3. Механический отбор.
Отбирают каждый двадцатый (сотый) экземпляр.
4. Серийный отбор.
В выборку подбираются экземпляры, произведенные на каком–то
производстве в определенный промежуток времени.
В дальнейшем под генеральной совокупностью мы будем
подразумевать не само множество объектов, а множество значений
случайной величины, принимающей числовое значение на каждом из
объектов. В действительности генеральной совокупности как множества
объектов может и не существовать. Например имеет смысл говорить о
множестве деталей, которые можно произвести, используя данный
технологический процесс. Используя какие–то известные нам
характеристики данного процесса, мы можем оценивать параметры этого
несуществующего множества деталей. Размер детали – это случайная
величина, значение которой определяется воздействием множества
факторов, составляющих технологический процесс. Нас, например, может
интересовать вероятность, с которой эта случайная величина принимает
значение, принадлежащее некоторому интервалу. На этот вопрос можно
ответить, зная закон распределения этой случайной величины, а также ее
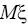
параметры, такие как и .
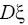
Итак, отвлекаясь от понятия генеральной совокупности как
множества объектов, обладающих некоторым признаком, будем
рассматривать генеральную совокупность как случайную величину ,
закон распределения и параметры которой определяются с помощью
выборочного метода.
Рассмотрим выборку объема n, представляющую данную
генеральную совокупность. Первое выборочное значение x1 будем
рассматривать как реализацию, как одно из возможных значений
случайной величины 1, имеющей тот же закон распределения с теми же
параметрами, что и случайная величина . Второе выборочное значение x₂
– одно из возможных значений случайной величины 2 с тем же законом
распределения, что и случайна величина . То же самое можно сказать о
значениях x₃, x₄,..., x_n .
Таким образом на выборку будем смотреть как на совокупность
независимых случайных величин 1, 2, ..., n, распределенных так же,
как и случайная величина , представляющая генеральную
совокупность. Выборочные значения x₁, x₂,..., x_n– это значения,
которые приняли эти случайные величины в результате 1-го, 2-го, ...,
n-го эксперимента.