Основной задачей математической статистики является разработка
методов получения научно обоснованных выводов о массовых явлениях и
процессах из данных наблюдений и экспериментов. Эти выводы и
заключения относятся не к отдельным испытаниям, из повторения
которых складывается данное массовое явление, а представляют собой
утверждения об общих вероятностных характеристиках данного процесса,
то есть о вероятностях, законах распределения, математических
ожиданиях, дисперсиях и т. д. Такое использование фактических данных
как раз и является отличительной чертой статистического метода.
Пусть мы располагаем сведениями (обычно довольно
ограниченными), например, о числе дефектных изделий в изготовленной в
определенных условиях продукции или о результатах испытаний
материалов на разрушение и т. п. Собранные нами данные могут
представлять непосредственный интерес в смысле информации о качестве
той или иной партии продукции. Статистические же проблемы возникают
тогда, когда мы на основе той же информации начинаем делать выводы
относительно более широкого круга явлений. Так например нас может
интересовать качество технологического процесса, для чего мы оцениваем
вероятность получения в нем дефектного изделия или среднюю
долговечность изделия. В этом случае мы рассматриваем собранный
материал не ради его самого, а лишь как некую пробную группу или
выборку, представляющую только серии из возможных результатов,
которые мы могли бы встретить при продолжении наблюдений массового
процесса в данной обстановке. Выводы и оценки, основанные на
материале наблюдений, отражают случайный состав пробной группы и
поэтому считаются приблизительными оценками вероятностного
характера. Во многих случаях теория указывает, как наилучшим способом
использовать имеющуюся информацию для получения по возможности
более точных и надежных характеристик, указывая при этом степень
надежности выводов, объясняющуюся ограниченностью запаса сведений.
В математической статистике рассматриваются две основные
категории задач: оценивание и статистическая проверка гипотез. Первая
задача разделяется на точечное оценивание и интервальное оценивание
параметров распределения. Например может возникнуть необходимость
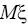
по наблюдениям получить точечные оценки параметров и . Если
мы хотим получить некоторый интервал, с той или иной степенью
достоверности содержащий истинное значение параметра, то это задача
интервального оценивания.
Вторая задача – проверка гипотез – заключается в том, что мы
делаем предположение о распределении вероятностей случайной
величины (например, о значении одного или нескольких параметров
функции распределения) и решаем, согласуются ли в некотором смысле
эти значения параметров с полученными результатами наблюдений.