Проверка статистической гипотезы о математическом ожидании нормального распределения при известной
дисперсии.
Пусть имеется нормально распределенная случайная величина ,
определенная на множестве объектов некоторой генеральной
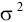
совокупности. Известно, что = . Математическое ожидание
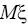
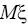
неизвестно. Допустим, что имеются основания предполагать, что = a,
где a – некоторое число (такими основаниями могут быть ограниченные
сведения об объектах генеральной совокупности, опыт исследования
подобных совокупностей и т. д.). Будем считать также, что имеется другая
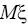
информация, указывающая на то, что = a₁, где a₁ > a.
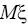
I. Выдвигаем нулевую гипотезу H₀: = a;
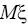
при конкурирующей гипотезе H₁: = a₁.
Делаем выборку объема n: x₁, x₂,..., x_n . В основе проверки лежит тот
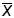
факт, что случайная величина (выборочная средняя) распределена по
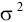
нормальному закону с дисперсией /n и математическим ожиданием,
равным a в случае справедливости H₀, и равным a₁ в случае
справедливости H₁.
Очевидно, что если величина x оказывается достаточно малой, то
это дает основание предпочесть гипотезу H0 гипотезе H₁. При достаточно
большом значении x более вероятна справедливость гипотезы H₁. Задачу
можно было бы поставить так: требуется найти некоторое критическое
число, которое разбивало бы все возможные значения выборочной
средней ( в условиях данной задачи это все действительные числа ) на два
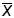
полубесконечных промежутка. При попадании в левый промежуток
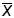
следовало бы принимать гипотезу H₀, а при попадании в правый
промежуток предпочтение следовало бы оказать гипотезе H₁. Однако на
самом деле поступают несколько иначе.
В качестве статистического критерия выбирается случайная
величина



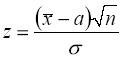
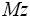
распределенная по нормальному закону , причем = 0 и Dz = 1 ( это
следует из свойств математического ожидания и дисперсии ) в случае
справедливости гипотезы H₀. Если справедлива гипотеза H₁, то
.
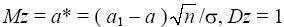