Можно установить взаимно-однозначное соответствие между всеми парами чисел (x:y) (или
множеством исходов) и множеством точек квадрата со
стороной, равной 1, на координатной плоскости, где начало
координат соответствует числу 12 по оси X и по оси Y, как
изображено на рисунке 6. Здесь, например, точка А
соответствует исходу, заключающемуся в том, что первый
пришел в 12.30, а второй - в 13.00. В этом случае, очевидно,
встреча не состоялась.
Если первый пришел не позже второго (y
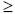
x), то
встреча произойдет при условии 0

y - x

1/6 (10 мин.- это 1/6 часа).
Если второй пришел не позже первого (x
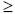
y), то
встреча произойдет при условии 0

x - y

1/6..
Между множеством исходов, благоприятствующих
встрече, и множеством точек области
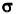
, изображенной на
рисунке 7 в заштрихованном виде, можно установить
взаимно-однозначное cоответствие.
Искомая вероятность p равна отношению площади
области
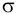
к площади всего квадрата.. Площадь квадрата
равна единице, а площадь области
можно определить как
разность единицы и суммарной площади двух
треугольников, изображенных на рисунке 7. Отсюда следует: