Рассмотрим случайный эксперимент, заключающийся в том, что подбрасывается
игральная кость, сделанная из неоднородного материала. Ее центр тяжести не
находится в геометрическом центре. В этом случае мы не можем считать исходы
(выпадение единицы, двойки и т.д.) равновероятными. Из физики известно, что кость
более часто будет падать на ту грань, которая ближе к центру тяжести. Как определить
вероятность выпадения, например, трех очков? Единственное, что можно сделать, это
подбросить эту кость n раз (где n-достаточно большое число, скажем n=1000 или
n=5000), подсчитать число выпадений трех очков n3 и считать вероятность исхода,
заключающегося в выпадении трех очков, равной n3/n - относительной частоте
выпадения трех очков. Аналогичным образом можно определить вероятности
остальных элементарных исходов — единицы, двойки, четверки и т.д. Теоретически
такой образ действий можно оправдать, если ввести статистическое определение
вероятности.
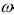
Вероятность P(i) определяется как предел относительной частоты появления
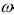
исхода i в процессе неограниченного увеличения числа случайных экспериментов n,
то есть



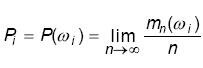
где m_n(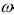_i) – число случайных экспериментов (из общего числа n произведенных
случайных экспериментов), в которых зарегистрировано появление элементарного
исхода 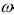_i.
Так как здесь не приводится никаких доказательств, мы можем только
надеяться, что предел в последней формуле существует, обосновывая надежду
жизненным опытом и интуицией.