Вычислять вероятности P(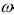_i ) можно, используя априорный подход, который
заключается в анализе специфических условий данного эксперимента (до проведения самого
эксперимента).
Возможна ситуация, когда пространство элементарных исходов состоит из
конечного числа N элементарных исходов, причем случайный эксперимент таков, что
вероятности осуществления каждого из этих N элементарных исходов представляются
равными. Примеры таких случайных экспериментов: подбрасывание симметричной
монеты, бросание правильной игральной кости, случайное извлечение игральной карты из
перетасованной колоды. В силу введенной аксиомы вероятности каждого элементарного
исхода в этом случае равны 1/N . Из этого следует, что если событие А содержит N_A
элементарных исходов, то в соответствии с определением (*)



В данном классе ситуаций вероятность события определяется как отношение
числа благоприятных исходов к общему числу всех возможных исходов.
Пример. Из набора, содержащего 10 одинаковых на вид электроламп, среди которых 4
бракованных, случайным образом выбирается 5 ламп. Какова вероятность, что среди
выбранных ламп будут 2 бракованные?
Прежде всего отметим, что выбор любой пятерки ламп имеет одну и ту же
вероятность. Всего существует C⁵₁₀ способов составить такую пятерку, то есть случайный
эксперимент в данном случае имеет C⁵₁₀ равновероятных исходов.
Сколько из этих исходов удовлетворяют условию "в пятерке две бракованные лампы",
то есть сколько исходов принадлежат интересующему нас событию?
Каждую интересующую нас пятерку можно составить так: выбрать две бракованные
лампы, что можно сделать числом способов, равным C²₄ . Каждая пара бракованных ламп
может встретиться столько раз, сколькими способами ее можно дополнить тремя не
бракованными лампами, то есть N³₆ раз. Получается, что число пятерок, содержащих две
бракованные лампы, равно C²₄•N³₆.
Отсюда, обозначив искомую вероятность через P, получаем: