Для построения полной и законченной теории случайного эксперимента или теории
вероятностей, помимо введенных исходных понятий случайного эксперимента,
элементарного исхода, пространства элементарных исходов, события, введем аксиому (пока
для случая конечного или счетного пространства элементарных исходов).
Каждому элементарному исходу 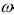_i пространства соответствует некоторая
неотрицательная числовая характеристика P_i шансов его появления, называемая
вероятностью исхода 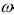_i , причем



(здесь суммирование ведется по всем i, для которых выполняется условие: ).
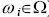
Отсюда следует, что 0 P_i 1для всех i.
Вероятность любого события А определяется как сумма вероятностей всех
элементарных исходов, благоприятствующих событию А. Обозначим ее Р(А).



Отсюда следует, что
1) 0 P(A) 1;
2) P=1;
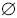
3) P()=0.

Будем говорить, что задано вероятностное пространство, если задано пространство
элементарных исходов и определено соответствие


Возникает вопрос: как определить из конкретных условий решаемой задачи
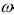
вероятность P(i ) отдельных элементарных исходов?