Разностью А\B или А-B событий А и B называется событие, состоящее из всех исходов
события А, не благоприятствующих событию B. Диаграмма
Венна разности событий А и B изображена на рисунке 4.
В условиях рассмотренного выше примера событие А\B
заключается в том, что первый стрелок попал в мишень, а второй
промахнулся.
Событие

называется достоверным (оно обязательно
происходит в результате случайного эксперимента).
Пустое множество
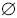
называется невозможным событием. Событие
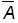
=

\A
называется противоположным событию А или дополнением события А.
События А и B называются несовместными, если нет
исходов, принадлежащих и А и B, то есть A

B =
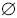
. На рисунке
5 изображены несовместные события А и B.
Непосредственно из введенных определений следуют
равенства: AU
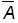
=

; A

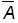
=
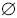
;
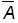

B•A

B ; A

B=A

B. Два
последних равенства называются формулами Де'Моргана.