Во втором случае говорят об обратной связи: с ростом случайная
величина имеет тенденцию к уменьшению или падению.
Если примерно одинаковый вклад в сумму дают и положительные и
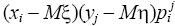
отрицательные произведения , то можно сказать, что в
сумме они будут “гасить” друг друга и ковариация будет близка к нулю. В этом
случае не просматривается зависимость одной случайной величины от другой.
Легко показать, что если



Действительно из (2) следует



Здесь использовано очень важное свойство математического ожидания:
математическое ожидание отклонения случайной величины от ее
математического ожидания равно нулю.
Доказательство (для дискретных случайных величин с конечным числом
значений).