Теперь каждому значению x
k случайной величины

можно поставить в
соответствие вероятность р
k = P(A
k) события А
k. Если такое соответствие
определено то будем говорить, что задан закон распределения дискретной
случайной величины

. Обычно закон распределения дискретной случайной
величины представляется в виде таблицы

(1)
В дальнейшем для краткости будем называть величину p
i вероятностью
значения х
i случайной величины. Отметим, что закон распределения содержит
всю информацию о случайной величине, и задать случайную величину можно,
просто представив её закон распределения.
Пусть две случайные величины
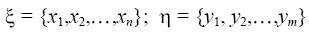
(2)
определены на одном и том же пространстве элементарных исходов. Если А
i
(i = 1,2,...,n) – событие, объединяющее все исходы, приводящие к значению х
i
случайной величины

, а В
j (j = 1,2,...,m) – событие, объединяющее все исходы,
приводящие к значению у
i случайной величины

, то можно определить
случайную величину

=

+

, которая принимает все возможные значения
z
ji= x
i + yj. Каждому такому значению =
jiслучайной величины

ставится в
соответствие вероятность p
ji , равная вероятности пересечения событий А
i и В
j:
