По формуле Бернулли можно подсчитать вероятности всех возможных частот:
x=0,1,2,3,4,5.
Заметим, что если в этой задаче считать, что белых шаров было 20000, а черных
60000, то очевидно p и q останутся неизменными. Однако в этой ситуации можно
пренебречь возвращением извлеченного шара после каждой выборки (при не слишком
больших значениях x) и считать вероятности всех частот: x=0,1,2,... по формуле
Бернулли.
Формула Бернулли при заданных числах p и n позволяет рассчитывать
вероятность любой частоты x (0

x

n). Возникает естественный вопрос: какой частоте
будет соответствовать наибольшая вероятность?
Предположим, что такая частота существует, и попытаемся ее определить из
условия, что вероятность этой частоты не меньше вероятности "предыдущей" и
"последующей" частот:
Первое неравенство (*) представляется в виде:
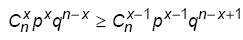
,
что эквивалентно
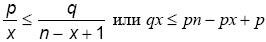
Отсюда следует:
Решая второе неравенство (1), получим
Таким образом, частота, имеющая наибольшую вероятность (чем вероятнейшая
частота), определяется двойным неравенством
Если np + p – целое число (тогда и np – q – целое число), то две частоты: x=np –
q и x=np + p обладают наибольшей вероятностью. Например, при
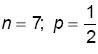
,
наивероятнейшие частоты: x = 3; x = 4.