Проверкой статистической значимости выборочной оценки
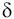
параметра

генеральной совокупности называется проверка
статистической гипотезы H
0:

= 0, при конкурирующей гипотезе
H
1:

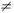
0. Если гипотеза H0 отвергается, то оценка
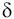
считается
статистически значимой.
Пусть имеются две случайные величины

и

, определенные на
множестве объектов одной и той же генеральной совокупности, причем
обе имеют нормальное распределение. Задача заключается в проверке
статистической гипотезы об отсутствии корреляционной зависимости
между случайными величинами

и

.
H
0:
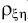
= 0;
H
1:
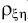
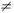
0.
Здесь
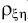
– коэффициент линейной корреляции.
Производится выборка объема n и вычисляется выборочный
коэффициент корреляции r. За статистический критерий принимается
случайная величина
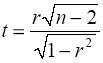
,
которая распределена по закону Стьюдента с n – 2 степенями свободы.
Отметим сначала, что все возможные значения выборочного
коэффициента корреляции r лежат в промежутке [–1;1]. Очевидно, что
относительно большие отклонения в любую сторону значений t от нуля
получаются при относительно больших, то есть близких к 1, значениях
модуля r. Близкие к 1 значения модуля r противоречат гипотезе H
0,
поэтому здесь естественно рассматривать двустороннюю критическую
область для критерия t.
По уровню значимости a и по числу степеней свободы n – 2 находим
из таблицы распределения Стьюдента значение t
кр. Если модуль
выборочного значения критерия t
в превосходит t
кр, то гипотеза H
0
отвергается и выборочный коэффициент корреляции считается
статистически значимым. В противном случае, то есть если |t
в| < t
кр и
принимается гипотеза H
0, выборочный коэффициент корреляции
считается статистически незначимым.