Выборочная оценка параметра, представляющая собой число,
называется точечной оценкой.
Выборочную дисперсию



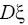
можно считать точечной оценкой дисперсии генеральной
совокупности.
Приведем еще один пример точечной оценки. Пусть каждый объект
генеральной совокупности характеризуется двумя количественными
признаками x и y. Например деталь может иметь два размера – длину и
ширину. Можно в различных районах измерять концентрацию вредных
веществ в воздухе и фиксировать количество легочных заболеваний
населения в месяц. Можно через равные промежутки времени
сопоставлять доходность акций данной корпорации с каким-либо
индексом, характеризующим среднюю доходность всего рынка акций. В
этом случае генеральная совокупность представляет собой двумерную
случайную величину , . Эта случайная величина принимает значения x, y
на множестве объектов генеральной совокупности. Не зная закона
совместного распределения случайных величин и , мы не можем
говорить о наличии или глубине корреляционной связи между ними,
однако некоторые выводы можно сделать, используя выборочный метод.
Выборку объема n в этом случае представим в виде таблицы, где
i-тый отобранный объект (i= 1,2,...n) представлен парой чисел x_i, y_i :