Во многих случаях мы располагаем информацией о виде закона
распределения случайной величины (нормальный, бернуллиевский,
равномерный и т. п.), но не знаем параметров этого распределения, таких
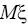
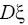
как , . Для определения этих параметров применяется выборочный
метод.
Пусть выборка объема n представлена в виде вариационного ряда.
Назовем выборочной средней величину



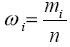
Величина называется относительной частотой значения признака
xi. Если значения признака, полученные из выборки не группировать и не
представлять в виде вариационного ряда, то для вычисления выборочной
средней нужно пользоваться формулой



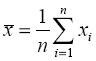
Естественно считать величину x выборочной оценкой параметра
.
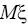