Пусть для объектов генеральной совокупности определен некоторый
признак или числовая характеристика, которую можно замерить (размер
детали, удельное количество нитратов в дыне, шум работы двигателя).
Эта характеристика – случайная величина

, принимающая на каждом
объекте определенное числовое значение. Из выборки объема n получаем
значения этой случайной величины в виде ряда из n чисел:
x1, x2,..., xn. (*)
Эти числа называются значениями признака.
Среди чисел ряда (*) могут быть одинаковые числа. Если значения
признака упорядочить, то есть расположить в порядке возрастания или
убывания, написав каждое значение лишь один раз, а затем под каждым
значением x
i признака написать число m
i, показывающее сколько раз
данное значение встречается в ряду (*):
то получится таблица, называемая дискретным вариационным рядом.
Число mi называется частотой i-го значения признака.
Очевидно, что x
i в ряду (*) может не совпадать с x
i в вариационном
ряду. Очевидна также справедливость равенства
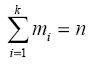
.
Если промежуток между наименьшим и наибольшим значениями
признака в выборке разбить на несколько интервалов одинаковой длины,
каждому интервалу поставить в соответствие число выборочных значений
признака, попавших в этот интервал, то получим интервальный
вариационный ряд. Если признак может принимать любые значения из
некоторого промежутка, то есть является непрерывной случайной
величиной, приходится выборку представлять именно таким рядом. Если в
вариационном интервальном ряду каждый интервал [a
i; a
i+1) заменить
лежащим в его середине числом (a
i+a
i+1)/2, то получим дискретный
вариационный ряд. Такая замена вполне естественна, так как, например,
при измерении размера детали с точностью до одного миллиметра всем
размерам из промежутка [49,5; 50,5), будет соответствовать одно число,
равное 50.