Законы условных распределений не отличаются друг от друга при =1,2,3
и совпадают с законом распределения случайной величины .
В данном случае и независимы.
Характеристикой зависимости между случайными величинами и
служит математическое ожидание произведения отклонений и от их
центров распределений (так иногда называют математическое ожидание
случайной величины), которое называется коэффициентом ковариации или
просто ковариацией.



Эту формулу можно интерпретировать так. Если при больших значениях
более вероятны большие значения , а при малых значениях более вероятны
малые значения , то в правой части формулы (2) положительные слагаемые
доминируют, и ковариация принимает положительные значения.
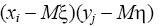
Если же более вероятны произведения , состоящие из
сомножителей разного знака, то есть исходы случайного эксперимента,
приводящие к большим значениям в основном приводят к малым значениям
и наоборот, то ковариация принимает большие по модулю отрицательные
значения.
В первом случае принято говорить о прямой связи: с ростом случайная
величина имеет тенденцию к возрастанию.