Отсюда
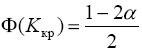
, и осталось воспользоваться таблицей функции Лапласа для нахождения числа K
кр.
Если величина z, полученная при выборочном значении x , попадает
в область принятия гипотезы (z <
кр), то гипотеза H
0 принимается
(делается вывод, что выборочные данные не противоречат гипотезе H
0).
Если величина z попадает в критическую область, то гипотеза H
0
отвергается.
В данной задаче может быть подсчитана мощность критерия:
Мощность критерия тем больше, чем больше разность a1– a.
II. Если в предыдущей задаче поставить другое условие:
H
0:
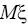
= a;
H
1:
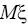
= a
1 , a
1 < a,
то сохранив смысл всех рассуждений, здесь
придется рассматривать левостороннюю
критическую область, как изображено на
рисунке 2. Здесь, как и в предыдущем
случае,
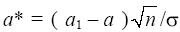
, а величина K
кр
определяется из формулы
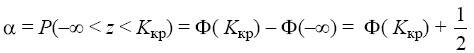
.