На рисунке 1. изображены графики
p₀(z) и p₁(z) – функций плотности распре-
деления случайной величины z при спра-
ведливости гипотез H₀ и H₁,
соответственно.



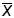
Если величина , полученная из
выборочных данных, относительно велика, то и величина z велика, что
является свидетельством в пользу гипотезы H₁. Относительно малые
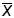
значения приводят к малым значениям z, что свидетельствует в пользу
гипотезы H₀. Отсюда следует, что должна быть выбрана правосторонняя
критическая область. По принятому уровню значимости a (например a =
0,05), используя то, что случайная величина z распределена по
нормальному закону, определим значение K_кр из формулы
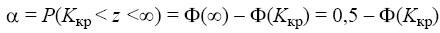