Пример 2. Даны две независимые случайные величины

и

с заданными
законами распределения
Определим случайные величины
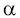
и
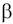
следующим образом:
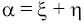
.
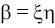
Выясним, являются ли независимыми случайные величины
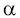
и
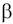
.
Составим закон распределения
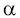
. Наименьшее значение
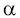
равняется 1.
Вероятность события
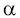
= 1 равна вероятности события (

= 0)

(

= 1), которая
в силу независимости

и

равна 1/3 • 1/4 = 1/12. Событие
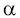
= 2 совпадает с
событием
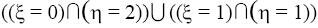
. Его вероятность равна
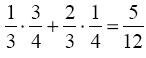
.
Максимальное значение
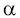
, равное 3, имеет вероятность 1/2. Таким образом,
закон распределения случайной величины
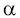
можно представить таблицей