Пусть имеется группа событий H
1, H
2,..., H
n , обладающая следующими
свойствами:
1) Все события попарно несовместны: H
i 
H
j =
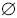
; i, j=1,2,...,n; i
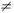
j
2) Их объединение образует пространство элементарных исходов

:

=H
1U H
2U ... U H
n.
В этом случае будем говорить, что H
1, H
2,...,H
n
образуют полную группу событий. Такие
события иногда называют гипотезами.
Пусть А - некоторое событие: А
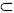

(диаграмма Венна представлена на рисунке 8).
Тогда имеет место формула полной
вероятности:
Доказательство. Очевидно: A = (A

H
1) U (A

H
2) U...U (A

H
n), причем все
события A

H
i (i = 1,2,...,n) попарно несовместны. Отсюда по теореме сложения
вероятностей получаем
Если учесть, что по теореме умножения P(A

H
i) = P(A/H
i) P(H
i) (i = 1,2,...,n), то
из последней формулы легко получить приведенную выше формулу полной
вероятности.