Как уже говорилось ранее, множество элементарных исходов может быть более,
чем счетным (то есть несчетным). В этом случае нельзя считать любое подмножество
множества событием.
Чтобы ввести определение случайного события, рассмотрим систему (конечную
или счетную) подмножеств A₁ ,A₂ A_n пространства элементарных исходов .
В случае выполнения трех условий:
1) принадлежит этой системе;
2) из принадлежности А этой системе следует принадлежность A этой системе;
3) из принадлежности A_i и A_j этой системе следует принадлежность A_i U A_j этой
системе
такая система подмножеств называется алгеброй.
Пусть — некоторое пространство элементарных исходов. Убедитесь в том,
что две системы подмножеств:
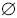
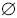
1) , ; 2) , А, A, (здесь А— подмножество ) являются алгебрами.
Пусть A₁ и A₂ принадлежат некоторой алгебре. Докажите, что A₁ \ A₂ и A₁ A₂
принадлежат этой алгебре.
Подмножество А несчетного множества элементарных исходов является
событием, если оно принадлежит некоторой алгебре.
Сформулируем аксиому, называемую аксиомой А.Н. Колмогорова.
Каждому событию соответствует неотрицательное и не превосходящее
единицы число P(А), называемое вероятностью события А, причем функция P(А)
обладает следующими свойствами:
1) Р()=1
2) если события A₁, A₂,..., A_n несовместны, то
P(A₁UA₂U...UA_n) = P (A₁) + P (A₂) +...+ P(A_n)
Если задано пространство элементарных исходов , алгебра событий и
определенная на ней функция Р, удовлетворяющая условиям приведенной аксиомы, то
говорят, что задано вероятностное пространство.
Это определение вероятностного пространства можно перенести на случай
конечного пространства элементарных исходов . Тогда в качестве алгебры можно
взять систему всех подмножеств множества .