Из пункта 2 приведенной аксиомы следует, что если A
1 и A
2 несовместные
события, то
Если A
1 и A
2 — совместные события, то A
1UA
2 =(A
1\ A
2)UA
2, причем очевидно,
что A
1\A
2 и A
2 — несовместные события. Отсюда следует:
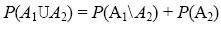
(*)
Далее очевидно: A
1 = (A
1\ A
2)U(A
1
A
2), причем A
1\ A
2 и A
1
A
2 - несовместные
события, откуда следует: P(A
1) = P(A
1\ A
2) + P(A
1?A
2) Найдем из этой формулы
выражение для P(A
1\ A
2) и подставим его в правую часть формулы (*). В результате
получим формулу сложения вероятностей:
Из последней формулы легко получить формулу сложения вероятностей для
несовместных событий, положив A
1
A
2 =
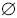
.
Пример. Найти вероятность вытащить туза или червовую масть при случайном
отборе одной карты из колоды в 32 листа.
Р( ТУЗ ) = 4/32 = 1/8; Р( ЧЕРВОВАЯ МАСТЬ ) = 8/32 = 1/4;
Р( ТУЗ ЧЕРВЕЙ ) = 1/32;
Р(( ТУЗ ) U (ЧЕРВОВАЯ МАСТЬ )) = 1/8 + 1/4 - 1/32 =11/32
Того же результата можно было достичь с помощью классического определения
вероятности, пересчитав число благоприятных исходов.