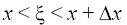Случайная величина, значения которой заполняют некоторый
промежуток, называется непрерывной.
В частных случаях это может быть не один промежуток, а объединение
нескольких промежутков. Промежутки могут быть конечными, полу-
бесконечными или бесконечными, например:
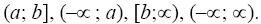
Вообще непрерывная случайная величина – это абстракция. Снаряд,
выпущенный из пушки, может пролететь любое расстояние, скажем, от 5 до 5,3
километров, но никому не придёт в голову измерять эту величину с точностью
до 0,0000001 километра (то есть до миллиметра), не говоря уже об абсолютной
точности. В практике такое расстояние будет дискретной случайной величиной,
у которой одно значение от другого отличается по крайней мере на 1 метр.
При описании непрерывной случайной величины принципиально
невозможно выписать и занумеровать все её значения, принадлежащие даже
достаточно узкому интервалу. Эти значения образуют несчётное множество,
называемое «континуум».
Если

– непрерывная случайная величина, то равенство

= х
представляет собой, как и в случае дискретной случайной величины, некоторое
случайное событие, но для непрерывной случайной величины это событие
можно связать лишь с вероятностью, равной нулю, что однако не влечёт за
собой невозможности события. Так например, можно говорить, что только с
вероятностью «нуль» снаряд пролетит 5245,7183 метра, или что отклонение
действительного размера детали от номинального составит 0,001059
миллиметра. В этих случаях практически невозможно установить, произошло
событие или нет, так как измерения величин проводятся с ограниченной
точностью, и в качестве результата измерения можно фактически указать лишь
границы более или менее узкого интервала, внутри которого находится
измеренное значение.
Значениям непрерывной случайной величины присуща некоторая
неопределенность. Например, нет практического смысла различать два
отклонения от номинального размера, равные 0,5 мм и 0,5000025 мм.
Вероятность, отличная от нуля, может быть связана только с попаданием
величины в заданный, хотя бы и весьма узкий, интервал. Здесь можно привести
сравнение с распределением массы вдоль стержня. Отсутствует масса,
сосредоточенная, скажем, в сечении, расположенном на расстоянии 20 см от
левого конца стержня, имеет смысл говорить лишь о массе, заключённой между
сечениями, проходящими через концы некоторого промежутка.
Пусть

– непрерывная случайная величина. Рассмотрим для некоторого
числа х вероятность неравенства