Осталось подобрать d таким, чтобы выполнялось равенство
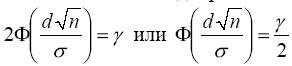
.
Для любого
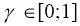
можно по таблице найти такое число t, что
Ф( t )= y / 2. Это число t иногда называют квантилем.
Теперь из равенства
определим значение
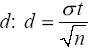
.
Окончательный результат получим, представив формулу (1) в виде:
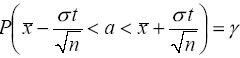
.
Смысл последней формулы состоит в следующем: с надежностью y
доверительный интервал
покрывает неизвестный параметр a =
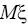
генеральной совокупности.
Можно сказать иначе: точечная оценка x определяет значение параметра
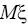
с точностью
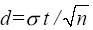
и надежностью y.
Задача. Пусть имеется генеральная совокупность с некоторой
характеристикой, распределенной по нормальному закону с дисперсией,
равной 6,25. Произведена выборка объема n = 27 и получено
средневыборочное значение характеристики
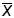
= 12. Найти доверительный
интервал, покрывающий неизвестное математическое ожидание
исследуемой характеристики генеральной совокупности с надежностью
y =0,99.
Решение. Сначала по таблице для функции Лапласа найдем значение
t из равенства Ф (t) = y / 2 = 0,495. По полученному значению
t = 2,58 определим точность оценки (или половину длины доверительного
интервала)
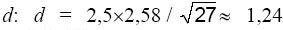
. Отсюда получаем искомый
доверительный интервал: (10,76; 13,24).