Такая выборочная оценка называется несмещенной.
Для доказательства несмещённости некоторых точечных оценок
будем рассматривать выборку объема n как систему n независимых
случайных величин 1, 2,... n , каждая из которых имеет тот же закон
распределения с теми же параметрами, что и случайная величина ,
представляющая генеральную совокупность. При таком подходе
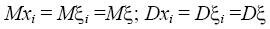
становятся очевидными равенства: для всех k = 1,2,...n.
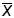
Теперь можно показать, что выборочная средняя есть
несмещенная оценка средней генеральной совокупности или , что то же
самое, математического ожидания интересующей нас случайной величины
:



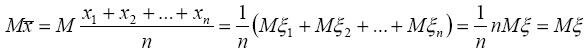
Выведем формулу для дисперсии выборочной средней:
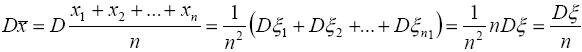