Задача. Найти интервал (x₁², X₂²), в
который случайная величина X² с 10-ю степенями свободы попадает с вероятностью, равной 0,9.
Решение. График плотности
распределения X² с 10-ю степенями
свободы схематично изображен на
рисунке 2. Будем считать, что площади заштрихованных областей (правая
область не ограничена справа) равны между собой. Примем условия:



тогда .
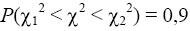
Равенства (1) сразу позволяют по таблице определить: X₂² = 18,3. Для
определения левой границы интересующего нас интервала придется
воспользоваться очевидным равенством P(X² > X₁²) = 0,95. Из таблицы 1.
определяем: X₁² = 3,94 , и теперь можно сформулировать ответ задачи:
значение случайной величины X² с вероятностью 0,9 принадлежит
интервалу (3,94; 18,3).