Введем понятие корреляционной зависимости между и .
Пусть задан закон совместного распределения двух случайных величин и (как в вышеприведенном примере), и условное математическое ожидание
меняется в зависимости от значения . Тогда принято говорить о
корреляционной зависимости от . Если условное математическое ожидание
есть линейная функция от , то между и имеется линейная
корреляционная связь или зависимость.
Как правило, говоря о корреляционной зависимости, имеют в виду
линейную корреляционную зависимость. Если имеется в виду нелинейная
корреляционная зависимость, то это особо оговаривают.
Можно дать определение корреляционной зависимости двух случайных
величин и как связи между тенденциями роста и . Например, между и
существует прямая корреляционная зависимость, если с ростом случайная
величина имеет тенденцию возрастать. (Это означает, что при больших
значениях с большей вероятностью встречаются большие значения ). Если
большим значениям n большей вероятностью соответствуют меньшие
значения , то есть с ростом случайная величина имеет тенденцию убывать,
говорят, что между и существует обратная корреляционная зависимость.
Глубина (или теснота) корреляционной зависимости (или связи)
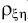
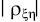
характеризуется коэффициентом . Чем ближе к единице, тем теснее
глубина корреляционной зависимости.
Чем ближе зависимость между условным математическим ожиданием и
случайной величиной к линейной, и чем теснее значения группируются
около условных математических ожиданий, тем глубже (теснее)
корреляционная связь.
Можно говорить о совместном распределении двух непрерывных
случайных величин. В большинстве случаев возможен переход от непрерывных
случайных величин к совместному распределению двух дискретных случайных
величин следующим образом.
Нужно разбить отрезок [a; b] изменения случайной величины на равные
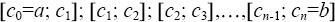
отрезки . За значение случайной величины
принять середину каждого отрезка.
Также надо поступить со случайной величиной , разбив ее область
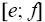
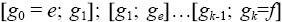
значений на равные отрезки , и приняв за
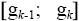
возможные значения середины отрезков . Таким образом мы
получили дискретные случайные величины ,
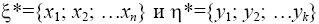
причем каждой паре (x_i; y_j) ставится в соответствие вероятность

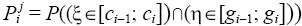
Таким образом мы придем к уже изученному материалу.