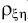
Коэффициент корреляции достигает своих предельных значений –1 и 1
в том и только в том случае, если совместное распределение и все
концентрируется на некоторой прямой в плоскости ; , то есть между и
имеется такая линейная зависимость.
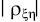
Если <1, то такой линейной зависимости нет. Все же по мере
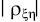
приближения к единице совместное распределение ; имеет тенденцию
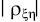
концентрироваться вблизи некоторой прямой линии и величину можно
считать мерой близости к полной линейной зависимости между и .

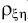
Пример. Рассчитаем коэффициент корреляции для случайных
величин при заданном законе совместного распределения