Аналогичные условные законы распределения случайной величины можно построить при всех остальных значениях , равных y²; y³,..., yⁿ ,ставя в соответствие числу x_i условную вероятность .

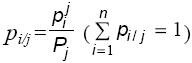
В таблице приведён условный закон распределения случайной величины при =y^j



Можно ввести понятие условного математического ожидания при =y^j



Заметим, что и равноценны. Можно ввести условное распределение при =x_i соответствием



Также можно ввести понятие условного математического ожидания случайной величины при =x_i :



Из определения следует, что если и независимы, то все условные законы распределения одинаковы и совпадают с законом распределения (напоминаем, что закон распределения определяется в таблице (*) первым и последним столбцом). При этом очевидно, совпадают все условные математические ожидания М(/ = y^j) при j = 1,2,...,k, которые равны М.
Если условные законы распределения при различных значениях различны, то говорят, что между и имеет место статистическая зависимость.