Часто результатом случайного эксперимента является число. Например,
можно подбросить игральную кость и получить одно из чисел: 1,2,3,4,5,6.
Можно подъехать к бензоколонке и обнаружить определённое число
автомашин в очереди. Можно выстрелить из пушки и измерить расстояние от
места выстрела до места падения снаряда. В таких случаях будем говорить, что
имеем дело со случайной величиной.
Каждому исходу случайного эксперимента поставим в соответствие
единственное число x
k — значение случайной величины. Тогда естественно
рассматривать случайную величину как функцию, заданную на множестве
исходов случайного эксперимента.
Случайная величина, которая может принимать лишь конечное или
счётное число значений, называется дискретной.
Случайные величины будем обозначать буквами греческого алфавита:

(кси),

(эта),... Значения случайной величины будем записывать в виде
конечной или бесконечной последовательности x
1, x
2,...x
n
Если говорится, что задана случайная величина

, это значит, что
каждому исходу

k случайного эксперимента поставлено в соответствие
единственное число x
k, что записывается в виде равенства x
k =

(
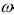 k
k).
Некоторые из значений xk могут совпадать, то есть различным исходам
может соответствовать одно и то же число x. Если все значения случайной
величины совпадают, то будем говорить, что случайная величина постоянна.
Пусть А
k — множество всех элементарных исходов, каждому из которых
соответствует значение x
k (k = 1,2,...,n) случайной величины

. Этот факт
можно записать в виде формулы
Таким образом, А
k – это событие (строго говоря, это верно лишь в случае
конечного или счётного числа исходов). Для каждого события Аk определим
число р
k 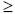
0, равное вероятности этого события: р
k = P(A
k). Очевидно, что