1. Если k – число, то
.
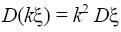
Доказательство.
2. Для попарно независимых случайных величин
1,
2,...,
n справедливо
равенство
Это свойство оставим без доказательства. Рекомендуем читателю рассмотреть
следующий пример.
Пусть
и
– независимые случайные величины с заданными законами
распределения:
Показать, что
.
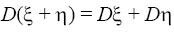
Математика