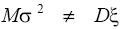
Так как , выборочная дисперсия не является несмещенной оценкой дисперсии генеральной совокупности.
Чтобы получить несмещенную оценку дисперсии генеральной
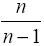
совокупности, нужно умножить выборочную дисперсию на . Тогда
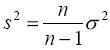
получится величина , называемая исправленной выборочной
дисперсией.



Пусть имеется ряд несмещенных точечных оценок одного и того же
параметра генеральной совокупности. Та оценка, которая имеет наимень-
шую дисперсию называется эффективной.
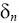
Полученная из выборки объема n точечная оценка параметра
генеральной совокупности называется состоятельной, если она сходится
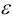
по вероятности к . Это означает, что для любых положительных чисел и
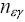
y найдется такое число , что для всех чисел n, удовлетворяющих
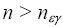
неравенству выполняется условие .
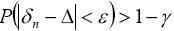
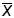
и s² являются несмещёнными, состоятельными и эффективными
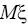
оценками величин и .
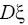