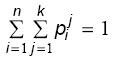Пусть пространство элементарных исходов случайного эксперимента таково, что каждому исходу 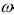_i ставиться в соответствие значение случайной величины , равное x_i и значение случайной величины , равное y^j.

Примеры:
1. Представим себе большую совокупность деталей, имеющих вид стержня. Случайный эксперимент заключается в случайном выборе одного стержня. Этот стержень имеет длину, которую будем обозначать и толщину— (можно указать другие параметры—объем, вес, чистота обработки, выраженная в стандартных единицах).

2. Если результат эксперимента—случайный выбор какого–либо предприятия в данной области, то за можно принимать объем производства отнесенный к количеству сотрудников, а за —объем продукции, идущей на экспорт, тоже отнесенной к числу сотрудников.

В этом случае мы можем говорить о совместном распределении случайных величин и или о “двумерной” случайной величине.
Если и дискретны и принимают конечное число значений ( – n значений, а – k значений), то закон совместного распределения случайных величин и можно задать, если каждой паре чисел x_i, y^j (где x_i принадлежит множеству значений , а y^j—множеству значений ) поставить в соответствие вероятность p_i^j, равную вероятности события, объединяющего все исходы 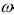_i^j (и состоящего лишь из этих исходов), которые приводят к значениям



Такой закон распределения можно задать в виде таблицы:



Очевидно