Во многих практических задачах встречаются случайные величины, у которых возможные
значения не ограничены сверху и снизу. В этом случае кривая распределения располагается над осью х и при
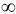
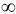
х -> и х -> - асимптотически приближается к этой оси, как изображено на
рисунке 1. Вероятность того, что случайная величина примет значение,
меньшее некоторого числа а, равна площади фигуры, заключённой между
кривой распределения и горизонтальной координатной осью слева от точки а.
Будем считать, что такая площадь существует.
Пусть – непрерывная случайная величина. Функция F(x), которая
определяется равенством



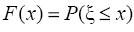
называется интегральной функцией распределения или просто функцией
распределения случайной величины . Непосредственно из определения
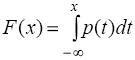
следует равенство . Формула производной определённого
интеграла по верхнему пределу в данном случае приводит к соотношению
F'(x) = p(x) . Плотность распределения р(х) называют дифференциальной
функцией распределения.
Функция распределения F(x) случайной величины имеет следующие
свойства.
1. F(x) — непрерывная возрастающая функция.
2.

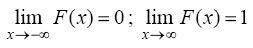
Свойства 1 и 2 вытекают непосредственно из определения функции F(x).
3. Приращение F(x) на промежутке (х1; х2) равно вероятности того, что
случайная величина принимает значение из этого промежутка: