Проверка гипотезы о равенстве дисперсий.

Гипотезы о дисперсии играют очень важную роль в экономико–
математическом моделировании, так как величина рассеяния
экспериментальных выборочных данных относительно рассчитанных
теоретических значений соответствующих параметров,
характеризующаяся дисперсией, дает возможность судить о пригодности
(адекватности) теории или модели, на основании которой строится теория.
Пусть нормально распределенная случайная величина определена
на некотором множестве, образующем генеральную совокупность, а
нормально распределенная случайная величина определена на другом
множестве, которое тоже составляет генеральную совокупность. Из обеих
совокупностей делаются выборки: из первой – объема 1, а из второй –
объема 2 (отметим, что объем выборки не всегда можно определить
заранее, как например в случае, если он равен количеству рыб, попавших в
сеть). По каждой выборке рассчитывается исправленная выборочная
дисперсия: s₁² для выборки из первой совокупности и s₂² для выборки из
второй совокупности.
Поставим задачу: с помощью выборочных данных проверить
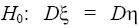
статистическую гипотезу . В качестве конкурирующей
гипотезы будем рассматривать идею, заключающуюся в том, что
дисперсия той совокупности, для которой исправленная выборочная
дисперсия оказалась наибольшей, больше дисперсии другой совокупности.
Критерий берется в следующем виде:



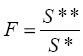
Здесь S**– наибольшая из двух оценок s₁² и s₂², а S*– наименьшая из тех
же двух оценок.
Критерий F распределен по закону Фишера с k₁ и k₂ степенями
свободы. Здесь



В этой задаче естественно рассматривать правостороннюю
критическую область, так как достаточно большие выборочные значения
критерия F свидетельствуют в пользу конкурирующей гипотезы.
При заданном уровне значимости q (обычно q =0,05 или q =0,01)
критическое значение F_кр определяется из таблицы распределения
Фишера. В случае F > F_кр гипотеза H₀ отвергается, а в случае F < F_кр –
принимается.
Пусть два множества некоторых объектов, обладающих
количественным признаком, подвергнуты выборочному контролю.
Значения количественного признака есть распределенные по нормальному
закону случайные величины, которые мы обозначим 1 и 2,
соответственно, для первого и для второго множеств. Из первого
множества сделана выборка объема n₁=21 и подсчитана исправленная
выборочная дисперсия, оказавшаяся равной 0,75. Из второго множества
сделана выборка объема n₂=11. Эта выборка дала значение исправленной
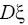
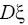
выборочной дисперсии, равное 0,25. Выдвигаем гипотезу H₀: 1=2.
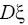
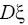
Конкурирующая гипотеза H₁ заключается в том, что 1>2. В данном
случае выборочное значение F_B критерия Фишера равно 3. При выбранном
уровне значимости q = 0,05 по числам степеней свободы k₁=20, k₂=10
находим по таблице распределения Фишера F_кр=2,77. Так как F_B > F_кр,
гипотеза о равенстве дисперсий должна быть отвергнута.