Чем меньше уровень значимости, тем меньше вероятность
отвергнуть проверяемую гипотезу H
0, когда она верна, то есть
совершить ошибку первого рода. Но с уменьшением уровня
значимости расширяется область принятия гипотезы H
0 и
увеличивается вероятность принятия проверяемой гипотезы, когда
она неверна, то есть когда предпочтение должно быть отдано
конкурирующей гипотезе.
Пусть при справедливости гипотезы H
0 статистический критерий K
имеет плотность распределения p
0(x), а при справедливости
конкурирующей гипотезы H
1 – плотность распределения p
1(x). Графики
этих функций приведены на рисунке 4. При некотором уровне значимости
находится критическое значение K
кp и правостороняя критическая
область. Если значение K
B, определенное по выборочным данным,
оказывается меньше, чем K
кp, то гипотеза H
0 принимается. Предположим,
что справедлива на самом деле конкурирующая гипотеза H
1. Тогда
вероятность попадания критерия в область принятия гипотезы H
0 есть
некоторое число
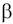
, равное площади фигуры, образованной графиком
функции p
1(x) и полубесконечной частью горизонтальной координатной
оси, лежащей слева от точки K
кp.
Очевидно, что
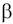
– это вероятность
того, что будет принята неверная
гипотеза H
0.
Принятие неверной
гипотезы называется ошибкой
второго рода. В рассмотренном случае число
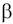
– это вероятность ошибки
второго рода. Число 1 –
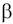
, равное вероятности того, что не совершается
ошибка второго рода, называется мощностью критерия. На рисунке 4
мощность критерия равна площади фигуры, образованной графиком
функции p
1(x).и полубесконечной частью горизонтальной координатной
оси, лежащей справа от точки K
кp.
Выбор статистического критерия и вида критической области
осуществляется таким образом, чтобы мощность критерия была
максимальной.
