В практических задачах часто приходится вычислять вероятности
различных событий, связанных с числом успехов в n испытаниях при
больших значениях n. В этих случаях вычисления по формуле по формуле
Бернулли становятся затруднительными. Трудности возрастают, когда
приходится суммировать вероятности P
n(x). К суммированию сводится
вычисление вероятностей событий вида k

x

l, как, например, в такой
задаче:Проводится 70 испытаний по схеме Бернулли с вероятностью
появления события А в одном испытании, равной 0,4. Найти вероятность
того, что событие А произойдет от 25 до 35 раз, то есть найти
P
n(25

x

35).
В отдельных случаях при больших n удается заменить формулу
Бернулли приближенными формулами. Такие формулы, которые
получаются при условии
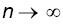
называются асимптотическими.
Если n достаточно велико, а p - величина очень малая, для формулы
Бернулли имеет место приближенная (асимптотическая) формула
Здесь
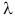
= np (
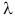
- греческая буква "лямбда"). Эта формула называется
формулой Пуассона. По формуле Пуассона вычисляются вероятности
числа появлений очень редких событий в массовых испытаниях.
Задача. Телефонная станция обслуживает 1000 абонентов. В течение
часа любой абонент независимо от остальных может сделать вызов с
вероятностью 0,05. Требуется найти вероятность того, что в течение часа
было не более 7 вызовов.
Здесь
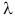
= np = 5. Пусть x - число вызовов. Нас интересуют значения
x, равные 0,1,....,7.
Если n достаточно велико, p не сильно отличается от 0,5, имеет
место формула Муавра-Лапласа, иногда называемая локальной
формулой Лапласа.
Из формулы видно, что одинаковые отклонения от величины np
вправо и влево здесь имеют одинаковые вероятности. В формуле Бернулли
это имеет место лишь при p=0.5.
