Если в написанной нами последовательности единица встречается х раз

Если в написанной нами последовательности единица встречается х раз (это
значит, что нуль встречается n-x раз), то вероятность соответствующего результата
будет pⁿq^n-x независимо от того, в каком порядке чередуются эти x единиц и n-x нулей.
Все события, заключающиеся в том, что в n испытаниях событие A произошло x
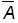
раз, а событие произошло n-x раз, являются несовместными. Поэтому для
вычисления вероятности объединения этих событий (или суммы этих событий), нужно
сложить вероятности всех этих событий, каждая из которых равна pⁿq^n-x . Всего таких
событий можно насчитать столько, сколько можно образовать различных
последовательностей длины n, содержащих x цифр "1" и n-x цифр "0". Таких
последовательностей получается столько, сколькими способами можно разместить x
цифр "1" (или n-x цифр "0") на n местах, то есть число этих последовательностей равно
C^x_n=C^n-x_n
Отсюда получается формула Бернулли:



По формуле Бернулли рассчитывается вероятность появления события A "x"раз в n
повторных независимых испытаниях, где p - вероятность появления события A в
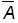
одном испытании, q - вероятность появления события в одном испытании.
Сформулированные условия проведения испытаний иногда называются "схемой
повторных независимых испытаний" или "схемой Бернулли"
Число x появления события A в n повторных независимых испытаниях
называется частотой.
Пример. Из урны, содержащей 2 белых и 6 черных шаров наудачу выбирается с
возвращением 5 раз подряд один шар. Подсчитать вероятность того, что 4 раза
появится белый шар.
В приведенных выше обозначениях n=8; p=1/4; q=3/4; x=5. Искомую
вероятность вычисляем по формуле Бернулли: