Используя определение дисперсии, для дискретной случайной величины
формулу вычисления дисперсии можно представить в таком виде:
Можно вывести ещё одну формулу для вычисления дисперсии:
Таким образом, дисперсия случайной величины равна разности мате-
матического ожидания квадрата случайной величины и квадрата её математи-
ческого ожидания.
Пример.
Найти дисперсию случайной величины, заданной законом распределения
Выше было показано, что M

= р. Легко видеть, что M
 2
2 = р. Таким образом,
получается, что
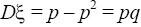
.
Дисперсия характеризует степень рассеяния значений случайной
величины относительно её математического ожидания. Если все значения
случайной величины тесно сконцентрированы около её математического
ожидания и большие отклонения от математического ожидания маловероятны,
то такая случайная величина имеет малую дисперсию. Если значения случайной
величины рассеяны и велика вероятность больших отклонений от
математического ожидания, то такая случайная величина имеет большую
дисперсию.
