Доверительный интервал для математического ожидания нормального распределения при неизвестной дисперсии.
Пусть

– случайная величина, распределенная по нормальному
закону с неизвестным математическим ожиданием
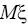
, которое обозначим
буквой a . Произведем выборку объема n. Определим среднюю
выборочную
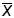
и исправленную выборочную дисперсию s
2 по известным
формулам.
Случайная величина
распределена по закону Стьюдента X
2 с n – 1 степенями свободы.
Задача заключается в том, чтобы по заданной надежности y и по
числу степеней свободы n – 1 найти такое число t
y , чтобы
выполнялось равенство
или эквивалентное равенство
Здесь в скобках написано условие того, что значение неизвестного
параметра a принадлежит некоторому промежутку, который и является
доверительным интервалом. Его границы зависят от надежности y , а
также от параметров выборки
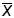
и s.
