Чтобы определить значение t

Чтобы определить значение t_y по величине y, равенство (2)
преобразуем к виду:



Теперь по таблице для случайной величины t, распределенной по закону
Стьюдента, по вероятности 1 – y и числу степеней свободы n – 1 находим
t_y . Формула (3) дает ответ поставленной задачи.
Задача. На контрольных испытаниях 20-ти электроламп средняя
продолжительность их работы оказалась равной 2000 часов при среднем
квадратическом отклонении (рассчитанном как корень квадратный из
исправленной выборочной дисперсии), равном 11-ти часам. Известно, что
продолжительность работы лампы является нормально распределенной
случайной величиной. Определить с надежностью 0,95 доверительный
интервал для математического ожидания этой случайной величины.
Решение. Величина 1 – y в данном случае равна 0,05. По таблице
распределения Стьюдента, при числе степеней свободы, равном 19,
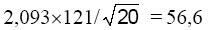
находим: t_y = 2,093. Вычислим теперь точность оценки: . Отсюда получаем искомый доверительный интервал:
(1943,4; 2056,6).