Доверительный интервал для математического ожидания нормального распределения при известной дисперсии.
Пусть случайная величина

(можно говорить о генеральной
совокупности) распределена по нормальному закону, для которого
известна дисперсия
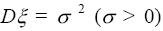
. Из генеральной совокупности (на
множестве объектов которой определена случайная величина) делается
выборка объема n. Выборка x
1, x
2,..., x
n рассматривается как совокупность
n независимых случайных величин, распределенных так же как

(подход,
которому дано объяснение выше по тексту).
Ранее также обсуждались и доказаны следующие равенства:
Достаточно просто доказать (мы доказательство опускаем), что
случайная величина
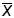
в данном случае также распределена по
нормальному закону.
Обозначим неизвестную величину
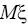
через a и подберем по
заданной надежности y число d > 0 так, чтобы выполнялось условие:
Так как случайная величина x распределена по нормальному закону
с математическим ожиданием
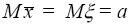
и дисперсией
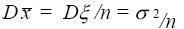
, получаем:
