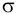
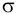
Пусть имеется нормально распределённая случайная величина с математическим ожиданием, равным а и дисперсией [img]https://teor-ver.ru/pic/s.jpg[/img ². Определим вероятность попадания [img]https://teor-ver.ru/pic/el.jpg[/img] в интервал (а – 3; а + 3), то есть вероятность того, что принимает значения, отличающиеся от математического ожидания не более, чем на три среднеквадратических отклонения.



По таблице находим Ф(3)=0,49865, откуда следует, что 2Ф(3) практически равняется единице. Таким образом, можно сделать важный вывод: нормальная случайная величина принимает значения, отклоняющиеся от ее математического ожидания не более чем на 3.
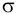
(Выбор числа 3 здесь условен и никак не обосновывается: можно было выбрать 2,8, 2,9 или 3,2 и получить тот же вероятностный результат. Учитывая, что Ф(2)=0,477, можно было бы говорить и о правиле 2–х “сигм”.)