Если все возможные значения случайной величины принадлежат интервалу
(а; b), то для р(х) – её плотности распределения справедливо равенство



Для удобства иногда считают функцию р(х) определённой для всех значений х,
полагая её равной нулю в тех точках х, которые не являются возможными
значениями этой случайной величины.
Плотностью распределения может служить любая интегрируемая
функция р(х), удовлетворяющая двум условиям:



Можно задавать случайную величину, задавая функцию р(х), удовлетворяющую
этим условиям.
В качестве примера рассмотрим случайную величину , равномерно
распределённую на промежутке [a; b]. В этом случае р(х) постоянна внутри
этого промежутка:



По свойству 2) функции р(х)



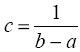
Отсюда График функции
р(х) представлен на рисунке 2.