Здесь

х – величина малого интервала.
Очевидно, что если
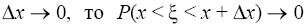
. Обозначим р(х)
предел отношения
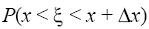
к при
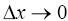
, если такой предел
существует:
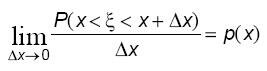
(1)
Функция р(х) называется плотностью распределения случайной величины. Из
формулы (1) следует равенство, справедливое для малых величин
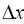
, которое
также можно считать определением функции р(х):
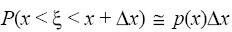
(2)
Очевидно, что p(x) – неотрицательная функция. Для определения вероятности
того, что случайная величина

примет значение из промежутка [a, b] конечной
длины, нужно выбрать на промежутке произвольные числа x
1, х2,..., хn
удовлетворяющие условию а=х0<эх1
промежуток [a, b] на n+1 частей, представляющих собой промежутки [х0, х1),
[х1, х2), ...,[хn, b]. Введём обозначения:
и составим сумму
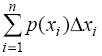
. Рассмотрим процесс, при котором число точек
разбиения неограниченно возрастает таким образом, что максимальная
величина
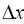
i стремится к нулю. Будем считать функцию p(x) непрерывной на
промежутке (а; b), тогда пределом суммы
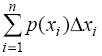
будет определённый
интеграл по промежутку [a; b] от функции p(x), равный искомой вероятности:
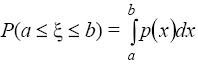
(3)
Это равенство можно также рассматривать как определение функции р(х).
Отсюда следует, что вероятность попадания случайной величины в любой
интервал (х1, х2) равна площади фигуры,
образованной отрезком [х1, х2] оси х,
графиком функции р(х) и вертикальными
прямыми х = х1, х = х2, как изображено на
рисунке 1.